Задача
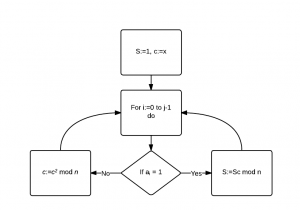
Быстрое возведение в степень
Предположим, например, что необходимо вычислить $x^{16}$. Можно просто начать с $x$ и 15 раз умножить его на $x$. Но тот же ответ можно получить всего за четыре умножения, если несколько раз возвести в квадрат получающийся результат, последовательно вычисляя $x^{2}$, $x^{4}$, $x^{8}$, $x^{16}$.
Эта же идея, в целом, применима к любому значению $n$ следующим образом. Запишем $n$ в виде числа в двоичной системе счисления (убирая нули слева). Затем заменим каждую «1» парой символов SX, а каждый «0» — символом S и вычеркнем крайнюю слева пару символов SX. Результат представляет собой правило вычисления $x^{n}$, в котором «S» трактуется как операция возведения в квадрат, а «X» — как операция умножения на $x$. Например, $n = 23$ имеет двоичное представление $10111$. Таким образом, мы формируем последовательность SXSSXSXSX, из которой удаляем начальную пару SX для получения окончательного правила SSXSXSX. Это правило гласит, что необходимо «возвести в квадрат, возвести в квадрат, умножить на $x$, возвести в квадрат, умножить на $x$, возвести в квадрат и умножить на $x$», т.е. последовательно вычислить значения $x^{2}$, $x^{4}$, $x^{5}$, $x^{10}$, $x^{11}$, $x^{22}$, $x^{23}$.
Вам нужно для заданного n сформулировать соответствующее правило быстрого возведения числа $x$ в степень $x^{n}$
Входные данные
Одно натуральное число $n$, не превышающее $2 \cdot 10^{9}$.
Выходные данные
Выведите строку для правила возведения числа $x$ в степень $n$ для получения $x^{n}$.
Тесты
| # | Входные данные | Выходные данные |
|---|---|---|
| 1 | 23 | SSXSXSX |
| 2 | 1 | |
| 3 | 16 | SSSS |
| 4 | 1000000 | SXSXSXSSXSSSSSXSSSXSSSSSS |
| 5 | 2018 | SXSXSXSXSXSSSSXS |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
import java.util.*; import java.lang.*; import java.io.*; class Main { public static void main (String[] args) throws java.lang.Exception { long n, k = 0, c = 0; Scanner S = new Scanner (System.in); n = S.nextLong(); while (n > 1){ long bit = n & 1; n >>= 1; k <<= 1; k |= bit; c += 1; } while (c != 0) { long bit = k & 1; k >>= 1; if (bit == 0) System.out.print("S"); else System.out.print("SX"); c -= 1; } } } |
Решение
С помощью первого цикла
while в переменную $k$ записываем перевернутый двоичный код числа $n$. Переменную $c$ используем как счётчик кол-ва бит в $n$. Во втором цикле
while выводим S или SX если правый бит $0$ или $1$ соответственно, теряя при это последнюю $1$ как и сказано по условию задачи.