e-olymp 1661. Рюкзак Алладина

09/09/2020 by Валентин Цушко

Условие

Попав в пещеру с сокровищами, наш Алладин не стал брать старую почерневшую лампу. Он кинулся собирать в свой рюкзак золотые монеты и драгоценные камни. Он бы, конечно, взял все, но чудес не бывает — слишком большой вес рюкзак может просто не выдержать.

Много раз он выкладывал одни вещи и на их место помещал другие, пытаясь как можно выше поднять стоимость взятых драгоценностей.

Требуется определить максимальную стоимость груза, который Алладин может поместить в свой рюкзак.

Будем считать, что в пещере имеются предметы $n$ различных типов, количество предметов каждого типа не ограничено. Максимальный вес, который может выдержать рюкзак, равен $w$. Каждый предмет типа $i$ имеет вес $w_{i}$ и стоимость $v_{i}$ $(i = 1, 2, \ldots, n)$.

Входные данные

В первой строке содержится два натуральных числа $w$ и $n$ $(1 \leqslant w \leqslant 250, 1 \leqslant n \leqslant 35)$ — максимальный вес предметов в рюкзаке и количество типов предметов. Следующие $n$ строк содержат по два числа $w_{i}$ и $v_{i}$ $(1 \leqslant w_{i} \leqslant 250, 1 \leqslant v_{i} \leqslant 250)$ — вес предмета типа $i$ и его стоимость.

Выходные данные

Выведите максимальную стоимость груза, вес которого не превышает $w$.

Тесты

№	Входные данные	Выходные данные
1	10 2 5 10 6 19	20
2	250 35 187 100 28 109 245 142 123 83 237 78 36 172 15 248 90 24 181 137 40 233 8 99 231 128 79 132 43 217 156 104 45 191 130 113 105 225 206 5 26 120 26 119 64 138 23 147 19 202 79 54 149 185 158 79 209 88 110 133 235 209 188 230 15 220 107 164 235 137 60 167	4067
3	35 4 20 4 1 2 10 8 7 6	70

Программный код

public class Main
{
	public static void main(String[] args) {
	    
	    java.util.Scanner in = new java.util.Scanner(System.in);
	    
		int w, n;
        int NegNum = -1;
        w = in.nextInt();
        n = in.nextInt();
        int WeiCos[][], s[];
        WeiCos = new int [n][2];
        s = new int [w + 1];
        for(int i = 0; i < n; i++){
            for(int j = 0; j < 2; j++){
                WeiCos[i][j] = in.nextInt();
            }
        }
        s[0] = 0;
        for(int j = 1; j <= w; j++){
            s[j] = NegNum;
        }
            for(int i = 0; i < n; i++){
            for(int j = WeiCos[i][0]; j <= w; j++){
                if(s[j - WeiCos[i][0]] != NegNum && s[j] < s[j - WeiCos[i][0]] + WeiCos[i][1]){
                    s[j] = s[j - WeiCos[i][0]] + WeiCos[i][1];
                }
            }
        }  
        int maxS = 0;
        for(int i = 1; i <= w; i++){
            maxS = Math.max(maxS, s[i]);
        }
        System.out.print(maxS);
	}
}

public class Main

{

public static void main(String[] args) {

java.util.Scanner in = new java.util.Scanner(System.in);

int w, n;

int NegNum = -1;

w = in.nextInt();

n = in.nextInt();

int WeiCos[][], s[];

WeiCos = new int [n][2];

s = new int [w + 1];

for(int i = 0; i < n; i++){

for(int j = 0; j < 2; j++){

WeiCos[i][j] = in.nextInt();

}

s[0] = 0;

for(int j = 1; j <= w; j++){

s[j] = NegNum;

}

for(int i = 0; i < n; i++){

for(int j = WeiCos[i][0]; j <= w; j++){

if(s[j - WeiCos[i][0]] != NegNum && s[j] < s[j - WeiCos[i][0]] + WeiCos[i][1]){

s[j] = s[j - WeiCos[i][0]] + WeiCos[i][1];

}

int maxS = 0;

for(int i = 1; i <= w; i++){

maxS = Math.max(maxS, s[i]);

}

System.out.print(maxS);

}

Решение

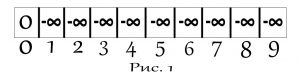
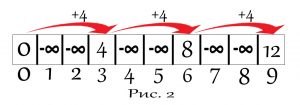
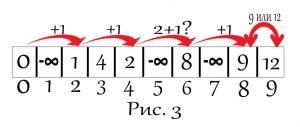
Допустим $w = 9$, $n = 2$, первый предмет $w_{1} = 3$, $n_{1} = 4$, а второй предмет $w_{2} = 2$, $n_{2} = 1$. После того как считаем условие в два одномерных или один двумерный массив (как вам удобнее). Создадим одномерный массив в котором его размер будет равен $w$ и первый элемент будет равен 0, а остальные будут равны минус бесконечности или как в нашем случае (в коде) -1, как показано на (рис. 1). И дальше как показано на (рис. 2) начиная с элемента с номером веса предмета мы прибавляем его стоимость к стоимости предыдущей как показано в коде s[j] = s[j - WeiCos[i][0]] + WeiCos[i][1];, если прошлый не минус бесконечность. И так же со вторым элементом, когда они пересекаются с первым мы их сравниваем и вписываем в массив, больший. И в самом конце проходим заново массив и выбираем самый больший элемент, где бы он ни был как показано на (рис. 3). И таким образом на последних позициях которые равняются весу, будут записаны самые дорогие комбинации, благодаря записи самых дорогих элементов в ячейки.

Ссылки:
Задача на e-olymp
Код на OnlineGDB
Код на Ideone
Засчитанное решение на e-olymp

e-olymp 3873. Счастливый номер

09/09/2020 by Валентин Цушко

Условие

Подавляющее большинство людей стараются найти закономерности, которые приносят удачу! Зуб акулы в ухе папуаса — к удачной рыбной ловле. Черная кошка, которая передумала перебегать вам дорогу — к отмене контрольной. Любимая игрушка у компьютера — к удаче в командном чемпионате по программированию.

Для большинства студентов несомненным является тот факт, что номер трамвайного билетика приносит удачу. А уж если такой билетик достался перед экзаменом, пятерка обеспечена! Главное тут — четко понимать, что такое счастливый билет. И почему, спрашивается, многие считают, что только номер автобусного или троллейбусного билета может приносить удачу своему владельцу?! Чем хуже, скажем, номер паспорта или номер кассового чека в гастрономе? Главное, чтобы номер был счастливым!

Витька всегда считал, что удачу приносят такие номера, в записи которых цифры идут в неубывающем порядке. Например, счастливыми являются номера $11111$ или $12345$. Даже номер $00000$ — тоже счастливый!

Интересно, сколько счастливых номеров существует для заданной длины записи числа? Напишите программу, которая это количество вычислит.

Входные данные

Входной файл содержит единственное целое число $N$, $(1 \leq N \leq 64)$, $N$ — длина числа, для которой нужно вычислить количество счастливых номеров.

Выходные данные

Вывести одно число — количество счастливых номеров.

Тесты

№	Входные данные	Выходные данные
1	2	55
2	4	715
3	3	220

Программный код

public class Main
{
    public static long factorial(int n){
        long a = 1;
        for (int i = (n + 9); i > n; i--) a = a * i;  // мы сократили, чтобы не пришлось делить огромные числа
        return a;
    }
	public static void main(String[] args) {
		

        java.util.Scanner in = new java.util.Scanner(System.in);
        
        int n;
        n = in.nextInt();
        long fact = 1;
        for (int i = 2; i <= 9; i++) fact = fact * i;
        System.out.print(factorial(n) / fact);
	}
}

public class Main

{

public static long factorial(int n){

long a = 1;

for (int i = (n + 9); i > n; i--) a = a * i; // мы сократили, чтобы не пришлось делить огромные числа

return a;

}

public static void main(String[] args) {

java.util.Scanner in = new java.util.Scanner(System.in);

int n;

n = in.nextInt();

long fact = 1;

for (int i = 2; i <= 9; i++) fact = fact * i;

System.out.print(factorial(n) / fact);

}

Решение

Для того, чтобы решить эту задачу, я начертил таблички (рис. 1.1) для всех вариантов $2$ значного числа и $1$ значного (рис. 1.2). Для $3$ значного аналогично, только рядов будет $3$. Из комбинаторики мы помним формулу: $C_n^m=\frac{n!}{m!(n-m)!}$, из которой мы получим: $(n + 9)! \over {9! \times n!}$. Потому-что из картинки мы видим что при 1 значном числе количество вариантов равно $10$. В коде я сразу сокращал на $n!$, чтобы не получались огромные числа.

рис 1.1

рис 1.2

Ссылки:
Задача на e-olymp
Код на OnlineGDB
Код на Ideone
Засчитанное решение на e-olymp

e-olymp 841. Спираль

09/09/2020 by Валентин Цушко

Условие

Вывести квадрат, состоящий из $N \times N$ клеток, заполненных числами от $1$ до $N^{2}$ по спирали.

Входные данные

В первой строке находится единственное число $N (2 \leq N \leq 100)$.

Выходные данные

Выводится $N$ строк по $N$ чисел, разделённых пробелами. Не допускается начинать спираль в ином, кроме верхнего левого, углу, закручивать спираль против часовой стрелки или изнутри наружу.

Тесты

№	Входные данные	Выходные данные
1	3	1 2 3 8 9 4 7 6 5
2	4	1 2 3 4 12 13 14 5 11 16 15 6 10 9 8 7
3	5	1 2 3 4 5 16 17 18 19 6 15 24 25 20 7 14 23 22 21 8 13 12 11 10 9
4	10	1 2 3 4 5 6 7 8 9 10 36 37 38 39 40 41 42 43 44 11 35 64 65 66 67 68 69 70 45 12 34 63 84 85 86 87 88 71 46 13 33 62 83 96 97 98 89 72 47 14 32 61 82 95 100 99 90 73 48 15 31 60 81 94 93 92 91 74 49 16 30 59 80 79 78 77 76 75 50 17 29 58 57 56 55 54 53 52 51 18 28 27 26 25 24 23 22 21 20 19

Программный код

class Main{
    public static void main (String[] args) throws java.lang.Exception {
    java.util.Scanner in = new java.util.Scanner(System.in);

    int n, m = 1;
    n = in.nextInt();
    int a[][];

    a = new int [n][n];

    if(n % 2 != 0){
        a[(n / 2)][(n / 2)] = (n * n); // если N - нечетное то находим центр матрицы и заполняем его числом N * N
    }

    for(int i = 0; i < (n / 2); i++){
        for(int j = i; j < (n - i); j++){ // (n - i) - чтоб с каждым разом сторона становилась меньше
            a[i][j] = m;
            m++;
        }
        for(int j = 1; j = i; j--){ // (n - 2) - i - отнимаем 1 чтоб не выходило за рамки массива и еще одну 1
            a[(n - i) - 1][(j)] = m; // потому-что предыдущий эл. уже заполнен.
            m++;
        }
        for(int j = ((n - i) - 2); j > i; j--){
            a[j][i] = m;
            m++;
        }
    }

    for(int i = 0; i < n; i++){
        for(int j = 0; j < n - 1; j++){
            System.out.print(a[i][j] + " ");
        }
        System.out.println(a[i][n - 1]);
    }
}
}

class Main{

public static void main (String[] args) throws java.lang.Exception {

java.util.Scanner in = new java.util.Scanner(System.in);

int n, m = 1;

n = in.nextInt();

int a[][];

a = new int [n][n];

if(n % 2 != 0){

a[(n / 2)][(n / 2)] = (n * n); // если N - нечетное то находим центр матрицы и заполняем его числом N * N

}

for(int i = 0; i < (n / 2); i++){

for(int j = i; j < (n - i); j++){ // (n - i) - чтоб с каждым разом сторона становилась меньше

a[i][j] = m;

m++;

}

for(int j = 1; j = i; j--){ // (n - 2) - i - отнимаем 1 чтоб не выходило за рамки массива и еще одну 1

a[(n - i) - 1][(j)] = m; // потому-что предыдущий эл. уже заполнен.

m++;

}

for(int j = ((n - i) - 2); j > i; j--){

a[j][i] = m;

m++;

}

for(int i = 0; i < n; i++){

for(int j = 0; j < n - 1; j++){

System.out.print(a[i][j] + " ");

}

System.out.println(a[i][n - 1]);

}

Решение

Для того чтобы решить эту задачу нам нужно определить способ заполнения. Первым делом, если $N$ — нечетное, то находим центр матрицы и заполняем его числом $N \times N $ a[(n / 2)][(n / 2)] = (n * n);. В условии написано, что “Не допускается начинать спираль в ином, кроме верхнего левого углу, закручивать спираль против часовой стрелки или изнутри наружу.”, то есть начинать мы будем с верхнего левого угла. Для этого мы сделаем цикл for(int i = 0; i < (n / 2); i++); , в котором сделаем 4 такта. Каждый такт заполняет определенную часть матрицы:

- 1 такт – заполняет верхнюю грань слева направо;
- 2 такт – заполняет правую грань сверху вниз;
- 3 такт – заполняет нижнюю грань справа налево;
- 4 такт – заполняет левую грань снизу вверх, как показано на рисунке ниже.

Выводим все как обычную матрицу, но с одним условием, после последнего элемента не должно стоять пробела, поэтому я вывел последний элемент отдельно и после него осуществил переход на новую строку.

Ссылки:
Задача на e-olymp
Код на OnlineGDB
Код на Ideone
Засчитанное решение на e-olymp

java@Cat

Учебные материалы по изучению основ языка програvмирования Java

Author Archives: Валентин Цушко

e-olymp 1661. Рюкзак Алладина

Условие

Входные данные

Выходные данные

Тесты

Программный код

Решение

e-olymp 3873. Счастливый номер

Условие

Входные данные

Выходные данные

Тесты

Программный код

Решение

e-olymp 841. Спираль

Условие

Входные данные

Выходные данные

Тесты

Программный код

Решение