Условие
По заданному натуральному числу $n$ вывести изображение размером $n\times n$, образованное символами звездочка и пробел как показано в примере.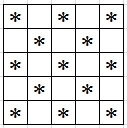
Входные данные
Одно натуральное число $n$.
Выходные данные
Вывести изображение $n \times n$.
Тесты
| № | Входные данные | Выходные данные | ||
| 1 | 2 |
|
||
| 2 | 3 |
|
||
| 3 | 4 |
|
||
| 4 | 5 |
|
||
| 5 | 6 |
|
Код программы
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
import java.util.*; import java.lang.*; import java.io.*; import java.util.Scanner; class Ideone { public static void main (String[] args) throws java.lang.Exception { long n; String s1 = "", s2 = ""; Scanner myObj = new Scanner(System.in); n = myObj.nextLong(); for (int i = 0; i < n; i++){//заполняем строки if (i % 2 == 0){ s1 += "*"; s2 += " "; } else { s2 += "*"; s1 += " "; } } for (int i = 0; i < n; i++){ if (i % 2 == 0){//выводим s1, если строка имеет четный номер System.out.println(s1); } else System.out.println(s2);//выводим s2, если строка имеет нечетный номер } } } |
Решение
Для того, чтобы вывести изображение как на рисунке достаточно заметить, что выводятся строки только двух видов и то поочерёдно. Первый вид — первым символом строки является $\ast$ и затем чередуется $\ast$ и пробел. Второй вид — первым символом строки является пробелом и затем чередуется $\ast$ и пробел. Мы заполняем две строки, по одной каждого вида. Нам остается только выводить строку необходимого нам вида, сделаем это в цикле.
Ссылки
Условие задачи на e-olymp
Код программы на ideone