Задача
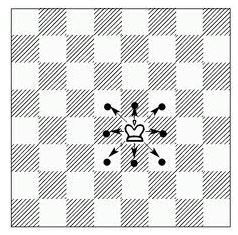
Одинокий король долго бродил по бесконечной шахматной доске. Известна последовательность из $n$ его ходов (вверх, вниз, влево, вправо, вверх-влево и т.п.) — возможные ходы короля показаны на рисунке снизу.
Определите, побывал ли король дважды на одном и том же поле за свои $n$ ходов.
Вводные данные
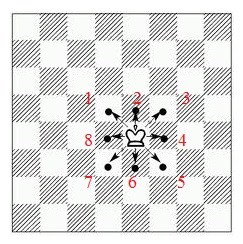
В первой строке задано общее число ходов короля $n$ $(0 \leq n \leq 1000)$. В последующих $n$ строках заданы направления перемещения короля: строка под номером $i+1$ задаёт направление перемещения короля на $i$-ом ходу.
Выходные данные
Выведите единственное число — номер хода, на котором король впервые попал на какую-то клетку во второй раз. Если же такое событие не произошло, то в первой строке выведите сообщение «Ok» (без кавычек), а во второй — манхэттенское расстояние между начальной и конечной точками путешествия одинокого короля.
Напоминаем, что манхэттенское расстояние между точками с координатами $(x_1, y_1)$ и $(x_2, y_2)$ определяется по формуле: $d=|x_2 — x_1| + |y_2 — y_1|$.
Тесты
| Входные данные | Выходные данные |
| $5\;1\;2\;4\;7\;4$ | $4$ |
| $5\;1\;2\;4\;6\;4$ |
$Ok$ $2$ |
| $8\;3\;3\;7\;7\;5\;5\;3\;3$ | $3$ |
| $12\;2\;3\;4\;1\;3\;2\;5\;6\;8\;2\;1\;7$ | $10$ |
| $9\;2\;2\;3\;3\;4\;4\;7\;7\;7$ |
$Ok$ 2 |
Код программы
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
import java.util.*; import java.lang.*; import java.io.*; class Main { public static void main (String[] args) throws java.lang.Exception { Scanner in = new Scanner(System.in); int[][] x = new int[2001][2001]; int n = in.nextInt(); int move; int xPos=1001, yPos=1001; for(int i = 0; i < n; i++) { move = in.nextInt(); if(x[xPos][yPos] == 1) { System.out.print(i); return; } else x[xPos][yPos]=1; if(move == 1) { xPos--; yPos++; } if(move == 2) { yPos++; } if(move == 3) { xPos++; yPos++; } if(move == 4) { xPos++; } if(move == 5) { xPos++; yPos--; } if(move == 6) { yPos--; } if(move == 7) { xPos--; yPos--; } if(move == 8) { xPos--; } } System.out.print("Ok" + "\n" + (Math.abs(xPos-1001)+Math.abs(yPos-1001))); } } |
Решение задачи
Создаем массив(изначально заполненный нулями). Задаем координаты короля по центру int xPos=1001, yPos=1001;. Затем в цикле вводим все ходы короля и проверяем был ли он уже в этой ячейке, если нет — ставим $1$, и вводим ход короля и задаем ему новые координаты, если да — выводим номер хода и завершаем программу. Если король ни разу не попал на ячейку, в которой уже был, то программа находим манхэттенское расстояние между начальными координатами и конечными. Задача решена.
Ссылки
Условие задачи на e-olymp
Код решения на ideone.com
