Задача
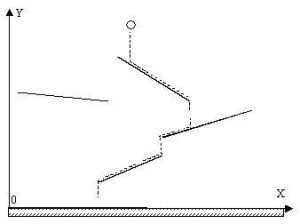
Как это выглядит на координатной плоскости
Капля дождя падает вертикально вниз с большой высоты на землю. На пути у капли могут встретиться препятствия, которые изменяют ее путь к земле.
Будем рассматривать двумерный вариант (на плоскости) этой задачи. Пусть препятствия – это наклонные непересекающиеся отрезки, а капля имеет точечные размеры. Капля падает вертикально вниз из точки, расположенной выше любого из препятствий. Если капля при падении соприкасается с отрезком-препятствием, то она стекает по отрезку вниз, пока не упадет вертикально вниз с меньшего по высоте конца отрезка.
Напишите программу, которая по координате $X_0$ точки появления капли над землей вычисляет координату $X$ точки соприкосновения капли с землей $Y=0$.
Входные данные: во входном файле в первой строке содержатся два целых числа через пробел – координата $X_0$ точки появления капли $(0 < X_0 < 10000)$ и количество отрезков-препятствий $N(0≤N≤100)$. Далее следует $N$ строк, каждая из которых содержит четыре разделенные пробелами числа $x_1, y_1, x_2, y_2$ – координаты левого и правого концов отрезка-препятствия $($все числа целые и находятся в диапазоне от $0$ до $10000, x_1 < x_2, y_1 ≠y_2)$. Отрезки не пересекаются и не соприкасаются.
Выходные данные: в выходной файл вывести одно целое число – координату $X$ точки соприкосновения капли с землей.
Тесты
| Входные данные | Выходные данные |
| 30 4 25 35 40 30 1 32 20 30 33 22 50 29 18 10 33 19 |
18 |
| 12 5 12 9 13 5 17 8 19 5 13 10 10 7 6 17 4 12 13 4 5 12 |
13 |
| 40 3 12 30 21 39 41 5 45 70 20 30 25 35 |
40 |
| 70 6 45 75 598 37 489 48 726 47 673 873 46 36 60 735 373 762 483 73 364 59 462 375 583 457 |
726 |
Код программы
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
import java.util.*; import java.lang.*; import java.io.*; class Main { static StreamTokenizer in = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in))); static PrintWriter out = new PrintWriter(System.out); static int nextInt() throws IOException { in.nextToken(); return (int)in.nval; } public static void main (String[] args) throws java.lang.Exception { int x = nextInt(), n = nextInt(); int N[][] = new int[n][4];; int tmp = 0; for (int i = 0; i < n; i++) for (int j = 0; j < 4; j++) N[i][j] = nextInt(); for (int i = 0; i < n; i++) for (int j = 0; j < n; j++) for (int q = 0; q < 4; q++) if ((N[i][1] > N[j][1] || N[i][3] > N[j][3]) || ( (N[i][1] == N[j][1] || N[i][3] == N[j][3] ) && (N[i][0] > N[j][0] || N[i][2] > N[j][2]) ) ) { tmp = N[i][q]; N[i][q] = N[j][q]; N[j][q] = tmp; } for (int i = 0; i < n; i++) { if (x >= N[i][0] && x <= N[i][2]) x = (N[i][1] < N[i][3]) ? N[i][0] : N[i][2]; for (int j = 0; j < 4; j++) N[i][j] = 0; } out.println(x); out.flush(); } } |
Решение задачи
Сортируем наш динамический массив по наибольшим координатам $y$ и, если $y$ равны, по координатам $x$.
Далее составим алгоритм решения задачи:
- Если $X\in[x_1,x_2]$, то наша капля пересечется с данной прямой. В противном случае мы просто игнорируем данное препятствие.
- Тогда мы сравниваем координаты $y_1$ и $y_2$, выбираем из них наименьшее и присваиваем соответствующую координату $x_1$ или $x_2$ координате
нашей капли $X$. - Повторяем до тех пор, пока не будут обработаны все препятствия и выводим последнюю присвоенную координату $X$ нашей капли, так как она и будет координатой $x$ соприкосновения капли с зимой.
Ссылки
Условие задачи на e-olymp.com
Решение задачи на ideone.com
