Задача
Циклический сдвиг
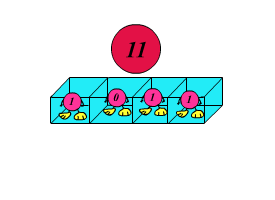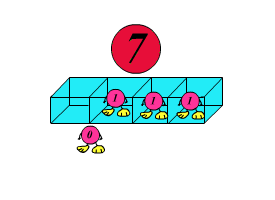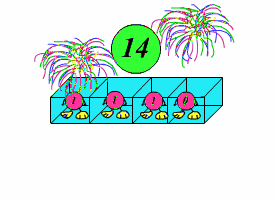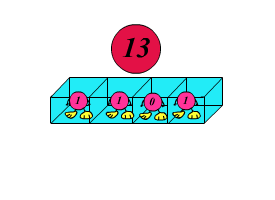
Запишем целое десятичное число $n$ в двоичной системе счисления и образуем все левые циклические сдвиги числа $n$, у которых первая цифра числа переносится в конец.
Например, если $n = 11$, то в двоичной системе это $1011_2$, его циклические сдвиги: $0111_2$, $1110_2$, $1101_2$, $1011_2$. Максимальное значение $m$ у всех полученных таким образом чисел будет иметь число $1110_2 = 14_{10}$.
Для заданного числа $n$ определить максимальное значение $m$.
Входные данные: одно число $n (1 ≤ n ≤ 2\cdot 10^9)$.
Выходные данные: искомое число $m$.
Тесты
| Входные данные | Выходные данные |
| 11 | 14 |
| 23 | 30 |
| 256 | 256 |
| 257 | 384 |
| 34132 | 43664 |
Код программы
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
import java.util.*; import java.lang.*; import java.io.*; class Main { public static void main (String[] args) throws java.lang.Exception { Scanner in = new Scanner(System.in); long in_val = in.nextInt(), tmp_val = in_val, power = 1; while (tmp_val != 0) { tmp_val /= 2; power *= 2; } tmp_val = in_val; long max_val = in_val; do{ in_val = in_val << 1; in_val = in_val % power + (in_val >= power ? 1 : 0); if (max_val < in_val) max_val = in_val; }while (tmp_val != in_val); System.out.println(max_val); } } |
Решение задачи
- Сначала мы находим степень двойки, большую данного числа;
- Далее мы циклически сдвигаем влево данное число на один бит и из полученных чисел выбираем наибольшее.
Ссылки
Условие задачи на e-olymp.com
Решение задачи на ideone.com
