Условие
Подавляющее большинство людей стараются найти закономерности, которые приносят удачу! Зуб акулы в ухе папуаса — к удачной рыбной ловле. Черная кошка, которая передумала перебегать вам дорогу — к отмене контрольной. Любимая игрушка у компьютера — к удаче в командном чемпионате по программированию.
Для большинства студентов несомненным является тот факт, что номер трамвайного билетика приносит удачу. А уж если такой билетик достался перед экзаменом, пятерка обеспечена! Главное тут — четко понимать, что такое счастливый билет. И почему, спрашивается, многие считают, что только номер автобусного или троллейбусного билета может приносить удачу своему владельцу?! Чем хуже, скажем, номер паспорта или номер кассового чека в гастрономе? Главное, чтобы номер был счастливым!
Витька всегда считал, что удачу приносят такие номера, в записи которых цифры идут в неубывающем порядке. Например, счастливыми являются номера $11111$ или $12345$. Даже номер $00000$ — тоже счастливый!
Интересно, сколько счастливых номеров существует для заданной длины записи числа? Напишите программу, которая это количество вычислит.
Входные данные
Входной файл содержит единственное целое число $N$, $(1 \leq N \leq 64)$, $N$ — длина числа, для которой нужно вычислить количество счастливых номеров.
Выходные данные
Вывести одно число — количество счастливых номеров.
Тесты
| № | Входные данные | Выходные данные |
| 1 | 2 | 55 |
| 2 | 4 | 715 |
| 3 | 3 | 220 |
Программный код
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
public class Main { public static long factorial(int n){ long a = 1; for (int i = (n + 9); i > n; i--) a = a * i; // мы сократили, чтобы не пришлось делить огромные числа return a; } public static void main(String[] args) { java.util.Scanner in = new java.util.Scanner(System.in); int n; n = in.nextInt(); long fact = 1; for (int i = 2; i <= 9; i++) fact = fact * i; System.out.print(factorial(n) / fact); } } |
Решение
Для того, чтобы решить эту задачу, я начертил таблички (рис. 1.1) для всех вариантов $2$ значного числа и $1$ значного (рис. 1.2). Для $3$ значного аналогично, только рядов будет $3$. Из комбинаторики мы помним формулу: $C_n^m=\frac{n!}{m!(n-m)!}$, из которой мы получим: $(n + 9)! \over {9! \times n!}$. Потому-что из картинки мы видим что при 1 значном числе количество вариантов равно $10$. В коде я сразу сокращал на $n!$, чтобы не получались огромные числа.
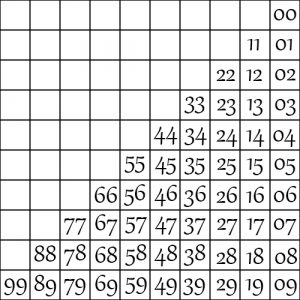
рис 1.1
рис 1.2
Ссылки:
Задача на e-olymp
Код на OnlineGDB
Код на Ideone
Засчитанное решение на e-olymp
