Описание АВЛ-дерева вы можете прочитать в Википедии.
Здесь представлен код реализации рекурсивного АВЛ-дерева. Отличается от обычно бинарного дерева тем, что у узлов есть высота и показатель балансировки. Балансировка может меняться при добавлении или удалении, и восстанавливается с помощью малого левого(правого), или большого левого(правого) поворотов. Как это выглядит можно увидеть в той же Википедии.
Показатель балансировки подсчитывается специальной функцией, как и показатель высоты.
Для возможности бегать по узлам дерева, есть приватные функция getHigherNode, getLowerNode. К которым есть доступ у узлов. К примеру мы в самой левой вершине дерева, либо мы лист, либо у нас есть правое поддерево. Если мы лист, то надо вернуть просто нашего предка. Если же есть правое поддерево. То надо вывести следующую вершину справа. Мы попали в эту вершину. Мы снова либо лист, либо есть правое поддерево, либо есть левое поддерево, либо сразу оба. Если мы лист, то нам надо подняться вверх по дереву, пока мы являемся правым сыном нашего предка, как только мы попадем в наш первоначальный самый маленький узел, мы перестаем быть правым сыном, значит нам пора остановиться, и вернуть отца самого маленького узла. Если же есть только правое поддерево(вернулись к моменту, где мы правый узел от самого маленького), то спускаемся снова вправо и имеем те же ситуации. Если же есть только левое поддерево, то заходим в него и действуем по тем же правилам. Если есть оба, то сначала пойдем в левое поддерево, после того, как мы там побываем и вернемся к узлу, нам надо будет продолжить обходить правое поддерево.
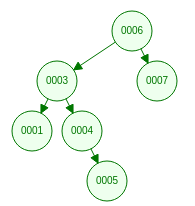
Попробуйте данный алгоритм действия, для этого дерева.
- Определите следующий элемент для узла 0001.
- Определите следующий элемент для узла 0003.
- Определите следующий элемент для узла 0004.
- Определите следующий элемент для узла 0005.
- Определите следующий элемент для узла 0007, зная, что предок корня — это null.
В коде присутствует поэтапный вывод дерева. Чтобы убедиться в корректности методов. Сначала вводятся так данные, чтобы сделать малый левый поворот. Потом так, чтобы сделать большой левый поворот и малый правый. После этого удаляются элементы так же, как и в бинарном дереве, только после удаление надо проверить показатель балансировки каждого из узлов, и если надо, то сбалансировать.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 |
/** * Created by green on 19.12.15. */ class AVL <Key extends Comparable<Key>, Value> { public class Node { private int h; private int balance; Key key; Value value; private Node left, right, father; public Node (Key key, Value value, Node father) { this.key = key; this.value = value; this.left = this.right = null; this.father = father; this.h = 1; this.balance = 0; } public Node next(){ return getHigherNode(this.key); } public Node previus(){ return getLowerNode(this.key); } } private Node root; //Возвращает ближайщий узел , больше данного ключа, //если узла с таким ключом нет, то возвращает ближайщий узел, больше заданного ключа. //Если нет ближайщего большего позначению,чем заданый ключ, то возвращает null private Node getHigherNode(Key key) { Node p = root; while (p != null) { int cmp = key.compareTo(p.key); if (cmp < 0) { if (p.left != null) p = p.left; else return p; } else { if (p.right != null) { p = p.right; } else { Node father = p.father; Node ch = p; while (father != null && ch == father.right) { ch = father; father = father.father; } return father; } } } return null; } //Возвращает ближайщий узел , меньше данного ключа, //если узла с таким ключом нет, то возвращает ближайщий узел, меньше заданного ключа. //Если нет ближайщего большего позначению,чем заданый ключ, то возвращает null private Node getLowerNode(Key key) { Node p = root; while (p != null) { int cmp = key.compareTo(p.key); if (cmp > 0) { if (p.right != null) p = p.right; else return p; } else { if (p.left != null) { p = p.left; } else { Node father = p.father; Node ch = p; while (father != null && ch == father.left) { ch = father; father = father.father; } return father; } } } return null; } public Node getFirstNode(){ return min(root); } public Node getLastNode(){ return max(root); } private int height(Node x, Node y){ if(x == null && y == null) return 0; else if(x == null) return y.h; else if(y == null) return x.h; else return Math.max(x.h, y.h); } private int balance(Node x, Node y){ if(x == null && y == null) return 0; else if(x == null) return - y.h; else if(y == null) return x.h; else return x.h - y.h; } private Node add (Node node,Key key, Value value, Node father){ if (node == null){ Node newnode = new Node(key,value, father); return newnode; } int compareResult = key.compareTo(node.key); if (compareResult > 0){node.right = add(node.right, key, value, node); node.h = height(node.left, node.right) + 1;} else if(compareResult < 0){node.left = add(node.left, key, value, node); node.h = height(node.left, node.right) + 1;} else{ node.value = value; } node.balance = balance(node.left, node.right); if(node.balance == -2){ node = leftRotation(node); }else if(node.balance == 2){ node = rightRotation(node); } return node; } private Node leftRotation(Node node) { if(node.right.right == null && node.right.left != null){ node.right = rightRotation(node.right); node = leftRotation(node); }else if(node.right.left == null || node.right.left.h <= node.right.right.h){ Node newnode = node.right; newnode.father = node.father; node.right = newnode.left; if(node.right != null) node.right.father = node; node.h = height(node.left, node.right)+1; node.father = newnode; node.balance = balance(node.left, node.right); newnode.left = node; node = newnode; node.balance = balance(node.left, node.right); node.h = height(node.left, node.right)+1; }else{ node.right = rightRotation(node.right); node = leftRotation(node); } return node; } private Node rightRotation(Node node){ if(node.left.right != null && node.left.left == null){ node.left = leftRotation(node.left); node = rightRotation(node); }else if(node.left.right == null || node.left.right.h <= node.left.left.h){ Node newnode = node.left; newnode.father = node.father; node.left = newnode.right; if(node.left != null) node.left.father = node; node.h = height(node.left, node.right)+1; node.father = newnode; node.balance = balance(node.left, node.right); newnode.right = node; node = newnode; node.balance = balance(node.left, node.right); node.h = height(node.left, node.right)+1; }else{ node.left = leftRotation(node.left); node = rightRotation(node); } return node; } public void add(Key key, Value value) { root = add(root, key, value, null); } private Node delete(Node node, Key key){ if(node == null) return null; int compareResult = key.compareTo(node.key); if(compareResult > 0){ node.right = delete(node.right, key); }else if(compareResult < 0){ node.left = delete(node.left, key); }else{ if(node.right == null && node.left == null){ node = null; }else if(node.right == null){ node.left.father = node.father; node = node.left; }else if(node.left == null){ node.right.father = node.father; node = node.right; }else{ if(node.right.left == null){ node.right.left = node.left; node.right.father = node.father; node.right.father = node.father; node.left.father = node.right; node = node.right; }else{ Node res = min(node.right); node.key = res.key; node.value = res.value; delete(node.right, node.key); } } } if(node != null) { node.h = height(node.left, node.right) + 1; node.balance = balance(node.left, node.right); if (node.balance == -2) { node = leftRotation(node); } else if (node.balance == 2) { node = rightRotation(node); } } return node; } public void delete(Key key) { root = delete(root, key); } public Key minKey(){ return min(root).key; } public Key maxKey(){ return max(root).key; } private Node min(Node node){ if(node.left == null) return node; return min(node.left); } private Node max(Node node){ if(node.right == null) return node; return min(node.right); } private Value get(Node node, Key key){ if(node == null) return null; int compareResult = key.compareTo(node.key); if(compareResult == 0){ return node.value; }else if(compareResult > 0){ return get(node.right, key); }else{ return get(node.left, key); } } public Value get(Key key) { return get(root, key); } private void print(Node node, int level) { if (node != null) { print(node.right,level+1); for (int i=0;i<level;i++) { System.out.print("\t"); } System.out.println(node.key + "->" + node.value+" h="+node.h+" balance="+node.balance); print(node.left,level+1); } } public void print() { print(root,0); } } public class avl_tree { public static void main(String[] args){ AVL<Integer, Integer> tree = new AVL<>(); tree.add(10,10); tree.print(); tree.add(11,11); tree.print(); tree.add(15,12); tree.print(); tree.add(13,12); tree.print(); tree.add(16,12); tree.print(); tree.add(12,12); tree.print(); tree.add(3,2); tree.print(); tree.add(1,1); tree.print(); tree.add(0,1); tree.print(); tree.add(2,1); tree.print(); tree.delete(13); tree.print(); tree.delete(10); tree.print(); for(AVL.Node e = tree.getFirstNode(); e != null; e = e.next()){ System.out.println(e.key); } } } |

Засчитано. Работа структуры проверена в других постах — т.к. алгоритмы, использующие АВЛ-дерево работают (засчитаны), то и АВЛ-дерево рабочее.