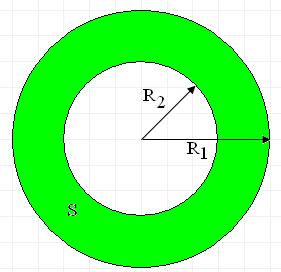
Заданы площадь кольца и радиус внешней окружности. Определить радиус внутренней окружности.
Входные данные
В одной строке заданы два вещественных числа: площадь кольца и радиус внешней окружности, величина которой не превышает $100$.
Выходные данные
Вывести радиус внутренней окружности с 2 десятичными знаками.
Тесты
| S | $R$ | $r$ |
| 50.2655 | 5 | 3.00 |
| 45 | 8 | 7.05 |
| 73.07 | 7.7 | 6.00 |
| 83.5 | 34 | 33.61 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
import java.util.*; import java.lang.*; import java.io.*; class Main { public static void main (String[] args) throws java.lang.Exception { double SR, Sr, r; double Pi = Math.PI; java.util.Scanner i = new java.util.Scanner(System.in); double S = i.nextDouble(); double R = i.nextDouble(); SR = Pi * R * R; Sr= SR - S; r=Math.sqrt(Sr/Pi); System.out.printf("%.2f",r); } } |
Решение
Для начала стоит напомнить, что площадь круга вычисляется по формуле $S=\pi R^2$.
С клавиатуры вводится площадь кольца $S$ и радиус большей окружности $R$
Зная значение радиуса большей окружности, можно найти площадь большего круга $S_R = \pi R^2$
Зная, что площадь малого круга и площадь кольца образуют площадь большого круга, найдём площадь малого круга $S_r = S_R — S$
Далее находим радиус малой окружности $r$ по формуле $r=\sqrt\frac{S_r}{\pi}$
