Задача

В пустой прямоугольной комнате длины [latex]А[/latex], ширины [latex]В[/latex] и высоты [latex]С[/latex] муха упала на пол и уснула. Паук, находящийся на одной из стен, или на полу, или на потолке, начал двигаться к ней по кратчайшему пути.

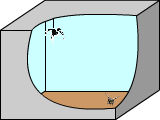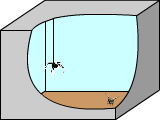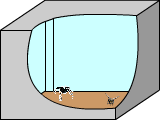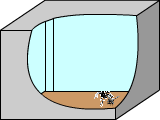
На какое расстояние он при этом переместится? Известно, что паук может передвигаться только по поверхности комнаты или же спускаться на паутине с потолка на пол, но только под прямым углом.

Входные данные

В первой строке заданы размеры комнаты [latex]A[/latex], [latex]B[/latex], [latex]C[/latex]. Во второй строке – координаты мухи на полу [latex]X1[/latex], [latex]Y1[/latex], [latex](0 ≤ X1 ≤ A[/latex], [latex]0 ≤ Y1 ≤ B)[/latex]. В третьей строке – координаты паука [latex]X2[/latex], [latex]Y2[/latex], [latex]Z2[/latex], [latex](0 ≤ X2 ≤ A[/latex], [latex]0 ≤ Y2 ≤ B[/latex], [latex]0 ≤ Z2 ≤ C)[/latex]. Все входные данные – целые не отрицательные числа, не превосходящие [latex]500[/latex].

Выходные данные

Одно число – расстояние, на которое переместится паук, посчитанное с точностью до 2-х знаков после запятой.

Тесты

Входные данные								Выходные данные
[latex]A[/latex]	[latex]B[/latex]	[latex]C[/latex]	[latex]X1[/latex]	[latex]Y1[/latex]	[latex]X2[/latex]	[latex]Y2[/latex]	[latex]Z2[/latex]	[latex]S[/latex]
[latex]4[/latex]	[latex]7[/latex]	[latex]3[/latex]	[latex]2[/latex]	[latex]1[/latex]	[latex]3[/latex]	[latex]7[/latex]	[latex]2[/latex]	[latex]8.06[/latex]
[latex]145[/latex]	[latex]26[/latex]	[latex]306[/latex]	[latex]12[/latex]	[latex]24[/latex]	[latex]0[/latex]	[latex]0[/latex]	[latex]305[/latex]	[latex]309.34[/latex]
[latex]26[/latex]	[latex]18[/latex]	[latex]53[/latex]	[latex]24[/latex]	[latex]15[/latex]	[latex]24[/latex]	[latex]1[/latex]	[latex]53[/latex]	[latex]58.52[/latex]
[latex]89[/latex]	[latex]89[/latex]	[latex]189[/latex]	[latex]12[/latex]	[latex]24[/latex]	[latex]0[/latex]	[latex]89[/latex]	[latex]16[/latex]	[latex]70.77[/latex]
[latex]18[/latex]	[latex]26[/latex]	[latex]145[/latex]	[latex]14[/latex]	[latex]2[/latex]	[latex]17[/latex]	[latex]26[/latex]	[latex]141[/latex]	[latex]147.14[/latex]

Код программы

import java.util.*;
import java.lang.*;
import java.io.*;

class Main
{
	private static double distance(long X1, long Y1, long X2, long Y2) 
	{
    	return Math.sqrt((X1-X2)*(X1-X2) + (Y1-Y2)*(Y1-Y2));
	}
	public static void main (String[] args) throws java.lang.Exception
	{
		Scanner in = new Scanner(System.in);
		long A = in.nextLong();
		long B = in.nextLong();
		long C = in.nextLong();
		long X1 = in.nextLong();
		long Y1 = in.nextLong();
		long X2 = in.nextLong();
		long Y2 = in.nextLong();
		long Z2 = in.nextLong();
		double S = 10000000;
		if (Z2 == 0)
    	{
    		S = distance(X1, Y1, X2, Y2);
    	}
		else
		{
			if (X2 == 0)
			{
				S = Math.min(distance(X1, Y1, -Z2, Y2), distance(X1, Y1, -Y2, -Z2));
				S = Math.min(S, distance(X1, Y1, Y2 - B, B + Z2));
			}
			if (X2 == A)
			{
				S = Math.min (distance(X1, Y1, Z2 + A, Y2), distance(X1, Y1, A + Y2, -Z2));
				S = Math.min(S, distance(X1, Y1, A + B - Y2, Z2 + B));
			}
			if (Y2 == 0)
			{
				S = Math.min(S, distance(X1, Y1, X2, -Z2));
				S = Math.min(S, distance(X1, Y1, -Z2, -X2));
				S = Math.min(S, distance(X1, Y1, A + Z2, X2 - A));
			}
			if (Y2 == B)
			{
				S = Math.min(S, distance(X1, Y1, X2, Z2 + B));
				S = Math.min(S, distance(X1, Y1, -Z2, X2 + B));
				S = Math.min(S, distance(X1, Y1, A + Z2, B + A - X2));
			}
			if ((Y2 != 0) && (Y2 != B) && (X2 != 0) && (X2 != A))
			{
				S = Math.min(C + distance(X1, Y1, X2, Y2), distance(X1, Y1, X2, -Y2 - C));
				S = Math.min(S, distance(X1, Y1, X2, 2*B - Y2 + C));
				S = Math.min(S, distance(X1, Y1, -X2 - C, Y2));
				S = Math.min(S, distance(X1, Y1, 2*A - X2 + C, Y2));
				S = Math.min(S, distance(X1, Y1, A + B + C - Y2, A + B - X2));
				S = Math.min(S, distance(X1, Y1, A + C + Y2, X2 - A));
				S = Math.min(S, distance(X1, Y1, -C - Y2, -X2));
				S = Math.min(S, distance(X1, Y1, Y2 - B - C, B + X2));
				S = Math.min(S, distance(X1, Y1, A + B - Y2, A + B + C - X2));
				S = Math.min(S, distance(X1, Y1, Y2 - B, B + C + X2));
				S = Math.min(S, distance(X1, Y1, -Y2, -C - X2));
				S = Math.min(S, distance(X1, Y1, A + Y2, -A - C + X2));
			}
		}
		System.out.printf("%.2f", S);
	}
}

import java.util.*;

import java.lang.*;

import java.io.*;

class Main

{

private static double distance(long X1, long Y1, long X2, long Y2)

{

return Math.sqrt((X1-X2)*(X1-X2) + (Y1-Y2)*(Y1-Y2));

}

public static void main (String[] args) throws java.lang.Exception

{

Scanner in = new Scanner(System.in);

long A = in.nextLong();

long B = in.nextLong();

long C = in.nextLong();

long X1 = in.nextLong();

long Y1 = in.nextLong();

long X2 = in.nextLong();

long Y2 = in.nextLong();

long Z2 = in.nextLong();

double S = 10000000;

if (Z2 == 0)

{

S = distance(X1, Y1, X2, Y2);

}

else

{

if (X2 == 0)

{

S = Math.min(distance(X1, Y1, -Z2, Y2), distance(X1, Y1, -Y2, -Z2));

S = Math.min(S, distance(X1, Y1, Y2 - B, B + Z2));

}

if (X2 == A)

{

S = Math.min (distance(X1, Y1, Z2 + A, Y2), distance(X1, Y1, A + Y2, -Z2));

S = Math.min(S, distance(X1, Y1, A + B - Y2, Z2 + B));

}

if (Y2 == 0)

{

S = Math.min(S, distance(X1, Y1, X2, -Z2));

S = Math.min(S, distance(X1, Y1, -Z2, -X2));

S = Math.min(S, distance(X1, Y1, A + Z2, X2 - A));

}

if (Y2 == B)

{

S = Math.min(S, distance(X1, Y1, X2, Z2 + B));

S = Math.min(S, distance(X1, Y1, -Z2, X2 + B));

S = Math.min(S, distance(X1, Y1, A + Z2, B + A - X2));

}

if ((Y2 != 0) && (Y2 != B) && (X2 != 0) && (X2 != A))

{

S = Math.min(C + distance(X1, Y1, X2, Y2), distance(X1, Y1, X2, -Y2 - C));

S = Math.min(S, distance(X1, Y1, X2, 2*B - Y2 + C));

S = Math.min(S, distance(X1, Y1, -X2 - C, Y2));

S = Math.min(S, distance(X1, Y1, 2*A - X2 + C, Y2));

S = Math.min(S, distance(X1, Y1, A + B + C - Y2, A + B - X2));

S = Math.min(S, distance(X1, Y1, A + C + Y2, X2 - A));

S = Math.min(S, distance(X1, Y1, -C - Y2, -X2));

S = Math.min(S, distance(X1, Y1, Y2 - B - C, B + X2));

S = Math.min(S, distance(X1, Y1, A + B - Y2, A + B + C - X2));

S = Math.min(S, distance(X1, Y1, Y2 - B, B + C + X2));

S = Math.min(S, distance(X1, Y1, -Y2, -C - X2));

S = Math.min(S, distance(X1, Y1, A + Y2, -A - C + X2));

}

System.out.printf("%.2f", S);

}

Решение задачи

Данная задача решается с помощью «разверток» комнаты: переход от трёхмерного пространства к двумерному.
Вид комнаты:

Рассмотрим такие случаи:

Паук находится на полу ([latex]Z_2 = 0[/latex]);
Паук находится на одной из стенок ([latex]X_2 = 0[/latex], или [latex]X_2 = A[/latex], или [latex]Y_2 = 0[/latex], или [latex]Y_2 = B[/latex] и [latex]Z_2 \neq 0[/latex]) либо на потолке ([latex]X_2 \neq 0[/latex], и [latex]X_2 \neq A[/latex], и [latex]Y_2 \neq 0[/latex], и [latex]Y_2 \neq B[/latex], и [latex]Z_2 = C[/latex]).

Первый случай тривиален и вычисляется по формуле [latex]\sqrt{(X_1 — X_2)^2 + (Y_1 — Y_2)^2}[/latex].
В случае, когда паук сидит на стенке, мы можем построить 3 развертки:
Допустим, паук находится на левой боковой стенке ([latex]X_2 = 0[/latex]). Остальные случаи аналогичны этому.

Паук ползет по этой стенке, затем по полу. Тогда развертка будет такой:
Паук ползет через ближнюю к нам стенку и по полу. Тогда развертка следующая:
Аналогичен предыдущему случаю, только через дальнюю от нас стенку.

По этим разверткам мы можем вычислить координаты паука и кратчайшее расстояние от него до мухи. Если же паук находится в одном из углов комнаты, то мы находим наименьшее расстояние из двух вариантов развертки.
Когда же паук сидит на потолке, не соприкасаясь ни с одной из стенок, у него есть 13 вариантов:

Паук спускается с потолка на паутине, затем ползет точно так же, как и в самом первом случае.
Паук ползет по потолку, по одной из стенок и по полу. Тогда развертка будет выглядеть следующим образом (потолок можно развернуть в 4 стороны — отсюда 4 случая):
Паук ползет по потолку, а затем по двум соседним стенкам и по полу. Таких случаев 8, поскольку порядок следования стенок, по которым тот ползет, также важен. Развертка одного из них:

По этим разверткам мы также можем вычислить координаты паука и кратчайшее расстояние от него до мухи.

Ссылки

Условие задачи на e-olymp
Задача Дьюдени о пауке и мухе
Код решения

java@Cat

Учебные материалы по изучению основ языка програvмирования Java

Tag Archives: паук и муха

e-olymp 74. Паук и муха — 2