Задача
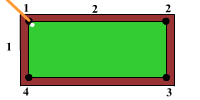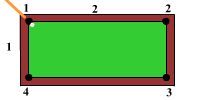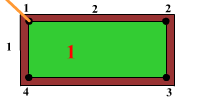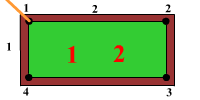
Биллиард представляет собой прямоугольник размерами $M \times N$, где $M$ и $N$ — натуральные числа. Из верхней левой лузы вылетает шар под углом $45^{\circ}$ к соседним сторонам. Лузы размещено только в углах биллиарда. Определите количество столкновений шара с бортами биллиарда, после которых он опять попадет в одну из луз, и номер лузы, в которую упадет шар. Считать, что трение отсутствует, столкновения абсолютно упругие, а шар — материальная точка.
Входные данные
Во входной строке два числа $M$ и $N$, $1 ≤ M, N ≤ 2000000000$. Нумерация луз по часовой стрелке, начиная с левой верхней лузы, из которой вылетел шар, согласно рисунка. $M$ — горизонтальная сторона биллиарда, $N$ — вертикальная сторона биллиарда.
Выходные данные
Два числа: количество отражений шара и номер лузы в которую упадет шар.
Тесты
| Входные данные | Выходные данные |
| 2 1 | 1 2 |
| 5 6 | 9 4 |
| 12 33 | 13 2 |
| 156 156 | 0 3 |
| 654 236 | 443 4 |
Код программы
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
import java.io.*; import java.util.*; import java.math.*; public class Main { public static void main(String[] args) { Scanner in = new Scanner(System.in); PrintWriter out = new PrintWriter(System.out); long m = in.nextLong(); long n = in.nextLong(); BigInteger bi1, bi2, bi3; bi1 = BigInteger.valueOf(m); bi2 = BigInteger.valueOf(n); bi3 = bi1.gcd(bi2); long g = bi3.longValue(); m /= g; n /= g; out.print((n + m - 2) + " "); if(n % 2 == 0 & m % 2 != 0) out.print(4); if(n % 2 != 0 & m % 2 != 0) out.print(3); if(n % 2 != 0 & m % 2 == 0) out.print(2); out.flush(); } } |
Решение
Чтобы решить эту задачу, необходимо сперва найти НОД значений $M$ и $N$ из условия. Для этого, нужно подключить библиотеку, содержащую функцию для нахождения НОД двух чисел, что мы и сделали в $3$ строке. Далее, в $17$ строке, введем перемененную g и присвоим ей значение НОД для $M$ и $N$. Теперь же, зная наш НОД, с его помощью можем подобрать эквивалентные числам из входного потока значения, которые будут, возможно, гораздо меньшими, чем изначальные, и работать уже с ними. В последующих строках находим искомые данные, причем количество отражений шара всегда находится по одной и той же формуле, в то время как номер лузы, в которую упадет шар, зависит от выполнения одного из трех условий, что и видно в коде.
Ссылки
Условие задачи на e-olymp
Код решения на Ideone
Решение этой же задачи на C++
