e-olymp 2670.Координаты соседей

27/12/2018 by Илья Черноморец

Задача

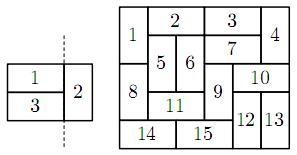
Для клетки с координатами $\left(x, y\right)$ в таблице размером $M\times N$ выведите координаты ее соседей. Соседними называются клетки, имеющие общую сторону.

Входные данные

Даны натуральные числа $M, N, x, y \left(1 \leqslant x \leqslant M \leqslant 109, 1 \leqslant y \leqslant N \leqslant 109\right).$

Выходные данные

В выходной файл выведите пары координат соседей этой клетки в произвольном порядке.

Тесты

Входные данные	Выходные данные
3 3 2 2	1 2 2 1 2 3 3 2
23 23 21 13	20 13 22 13 21 12 21 14
11 8 10 5	9 5 11 5 10 4 10 6

Код решения

import java.util.*;
import java.lang.*;
import java.io.*;
class Main
{
	public static void main (String[] args) throws java.lang.Exception
	{
		
		Scanner in = new Scanner(System.in);
                int n = in.nextInt();
                int m = in.nextInt();
                int x = in.nextInt();
                int y = in.nextInt();
		if (x > 1) System.out.print((x-1)+" "+y+"\n");
		if (x  1) System.out.print(x+" "+(y-1)+"\n");
		if (y < m) System.out.print(x+" "+(y+1)+"\n");
	}
}

import java.util.*;

import java.lang.*;

import java.io.*;

class Main

{

public static void main (String[] args) throws java.lang.Exception

{

Scanner in = new Scanner(System.in);

int n = in.nextInt();

int m = in.nextInt();

int x = in.nextInt();

int y = in.nextInt();

if (x > 1) System.out.print((x-1)+" "+y+"\n");

if (x 1) System.out.print(x+" "+(y-1)+"\n");

if (y < m) System.out.print(x+" "+(y+1)+"\n");

}

Решение

Для решения этой задачи стоит просмотреть все варианты координат соседних точек. То есть, нужно прибавить единицу к абсциссам и ординатам заданной точки. Но стоит учесть, что таблица у нас ограничена: $1 \leqslant x \leqslant M, 1 \leqslant y \leqslant N$

Ссылки

Ссылка на E-olymp
Ссылка на решение

e-olymp 3843. Простые

27/12/2018 by Илья Черноморец

Задача

Пусть $m$ и $n$ $\left(2 ≤ m < n ≤ 107\right)$ — целые числа. Рассмотрим следующее множество:

Prime $\left(m, n\right) = \lbrace{ p | p\;простое, m ≤ p ≤ n \rbrace}$.

Вычислить мощность множества Prime$\left(m, n\right)$.

Входные данные

Состоит из нескольких тестов. Два последовательных теста разделены пустой строкой. Для каждого теста в отдельной строке заданы числа $m$ и $n$.

Выходные данные

Для каждого теста вывести результат в отдельной строке. Результаты соседних тестов разделять пустой строкой. Для каждого теста вывести мощность множества Prime$\left(m, n\right)$.

Тесты

Входные данные	Выходные данные
2 20 70 110 5 150	8 10 33
7 2056 14 181 27 367	307 36 64
77 777 55 555 33 333	116 85 56

Входные данные

Выходные данные

2 20

70 110

5 150

7 2056

14 181

27 367

307

77 777

55 555

33 333

116

Код решения

import java.util.*;
import java.lang.*;
import java.io.*;
import java.util.Arrays;
import java.util.Scanner;

class Main
{
  public static void main (String[] args) throws java.lang.Exception
  {
     
     Scanner in = new Scanner(System.in);
    
     final int MAXN = 10000001;
     int simple[]=new int[MAXN+1];
     for(int i = 2; i <= MAXN; i++){
         simple[i] = 1;
     }
     for(int i = 2; i <= Math.sqrt(MAXN); i++){
         if(simple[i]==1){
             for(int j = i * i; j <= MAXN; j += i){
                 simple[j] = 0;
             }
         }
     }
 
     int count[]=new int[MAXN+1];
     int lastSum = 0;
     for(int i = 1; i < MAXN; i++){
         count[i] = lastSum + simple[i];
         lastSum = count[i];
     }
      while(in.hasNextInt()) {
        int m = in.nextInt();
    int n = in.nextInt();
        int answer = count[n] - count[m] + simple[m];
        System.out.println();
      System.out.println(answer);
      }
  }
}

import java.util.*;

import java.lang.*;

import java.io.*;

import java.util.Arrays;

import java.util.Scanner;

class Main

{

public static void main (String[] args) throws java.lang.Exception

{

Scanner in = new Scanner(System.in);

final int MAXN = 10000001;

int simple[]=new int[MAXN+1];

for(int i = 2; i <= MAXN; i++){

simple[i] = 1;

}

for(int i = 2; i <= Math.sqrt(MAXN); i++){

if(simple[i]==1){

for(int j = i * i; j <= MAXN; j += i){

simple[j] = 0;

}

int count[]=new int[MAXN+1];

int lastSum = 0;

for(int i = 1; i < MAXN; i++){

count[i] = lastSum + simple[i];

lastSum = count[i];

}

while(in.hasNextInt()) {

int m = in.nextInt();

int n = in.nextInt();

int answer = count[n] - count[m] + simple[m];

System.out.println();

System.out.println(answer);

}

Решение

Для решения этой задачи требуется завести большой массив типа bool и присвоить ему значение true. Затем проверяется, простое ли число, если это не так, то присваиваем значение false.
Затем нужно последовательно сосчитать мощность каждого множества простых чисел, то есть количество простых чисел от n до m, с помощью массива-счётчика: записывается в него прошлые и последующие элементы множества простых чисел.
После этого в цикле задаются нужные значения, считается ответ и выводится.

Ссылки

Ссылка на E-olymp
Ссылка на решение

e-olymp 1489. Шоколад

27/12/2018 by Илья Черноморец

Задача

Петя очень любит шоколад. И Маша очень любит шоколад. Недавно Петя купил шоколадку и теперь хочет поделиться ею с Машей. Шоколадка представляет собой прямоугольник $n \cdot m$, который полностью состоит из маленькихшоколадных долек — прямоугольников $2 \cdot 1$.

Петя делит шоколадку на две части, разламывая ее вдоль некоторой прямой, параллельной одному из краев шоколадки. Ни Петя, ни Маша не любят ломаные дольки, поэтому Петя хочет разломать шоколадку так, чтобы ни одна долька не была повреждена.

Помогите Пете поделиться шоколадкой с Машей.

Входные данные

В первой строке входного файла два целых числа $n$ и $m$ ($1 \le n, m \le 20$, хотя бы одно из чисел $n$ и $m$ — четно). Далее следуют $n$ строк по $m$ чисел в каждой — номера долек, в которые входят соответствующие кусочки шоколадки. Дольки имеют номера от $1$ до $\frac{n \cdot m}{2}$, и никакие две дольки не имеют одинаковые номера.

Выходные данные

В выходной файл выведите «$Yes$», если Петя может разломать шоколадку, не повредив дольки. Иначе выведите «$No$».

TESTS

Входные данные	Выходные данные
2 3 1 1 2 3 3 2	Yes
5 6 1 2 2 3 3 4 1 5 6 7 7 4 8 5 6 9 10 10 8 11 11 9 12 13 14 14 15 15 12 13	No
4 7 1 1 2 5 8 11 6 2 14 4 7 3 9 5 3 7 10 6 13 2 3 4 3 8 12 5 7 7	Yes

Код решения

import java.io.InputStream;
import java.io.InputStream;
import java.io.OutputStream;
import java.io.PrintWriter;
import java.util.Scanner;

public class Main {

    public static void main(String[] args) {
        new Resolver(System.in, System.out).solve();
    }

    public static class Resolver {

        private Scanner scanner;
        private PrintWriter writer;

        public Resolver(InputStream is, OutputStream os) {
            this.scanner = new Scanner(is);
            this.writer = new PrintWriter(os);
        }

        public void solve() {
            int rowCount = scanner.nextInt();
            int columnCount = scanner.nextInt();
            int[][] chocolate = new int[rowCount][columnCount];
            for (int i = 0; i < rowCount; i++) {
                for (int j = 0; j < columnCount; j++) chocolate[i][j] = scanner.nextInt();
            }
            check(chocolate, rowCount, columnCount);
            writer.flush(); writer.close();
        }

        private void check(int[][] chocolate, int rowCount, int columnCount) {
            if (BreakRow(chocolate, rowCount, columnCount) || BreakColumn(chocolate, rowCount, columnCount)) writer.println("Yes");
            else writer.println("No");
        }
        private boolean BreakRow(int[][] chocolate, int rowCount, int columnCount) {
            for (int i = 0; i < rowCount - 1; i++) {
                boolean okRow = true;
                for (int j = 0; j < columnCount; j++) {
                    if (chocolate[i][j] == chocolate[i + 1][j]) { okRow = false; break; }
                }
                if (okRow) return true;
            }
            return false;
        }
        private boolean BreakColumn(int[][] chocolate, int rowCount, int columnCount) {
            for (int i = 0; i < columnCount - 1; i++) {
                boolean okColumn = true;
                for (int j = 0; j < rowCount; j++) {
                    if (chocolate[j][i] == chocolate[j][i + 1]) { okColumn = false; break; }
                }
                if (okColumn) return true;
            }
            return false;
        }
    }
}

import java.io.InputStream;

import java.io.OutputStream;

import java.io.PrintWriter;

import java.util.Scanner;

public class Main {

public static void main(String[] args) {

new Resolver(System.in, System.out).solve();

}

public static class Resolver {

private Scanner scanner;

private PrintWriter writer;

public Resolver(InputStream is, OutputStream os) {

this.scanner = new Scanner(is);

this.writer = new PrintWriter(os);

}

public void solve() {

int rowCount = scanner.nextInt();

int columnCount = scanner.nextInt();

int[][] chocolate = new int[rowCount][columnCount];

for (int i = 0; i < rowCount; i++) {

for (int j = 0; j < columnCount; j++) chocolate[i][j] = scanner.nextInt();

}

check(chocolate, rowCount, columnCount);

writer.flush(); writer.close();

}

private void check(int[][] chocolate, int rowCount, int columnCount) {

if (BreakRow(chocolate, rowCount, columnCount) || BreakColumn(chocolate, rowCount, columnCount)) writer.println("Yes");

else writer.println("No");

}

private boolean BreakRow(int[][] chocolate, int rowCount, int columnCount) {

for (int i = 0; i < rowCount - 1; i++) {

boolean okRow = true;

for (int j = 0; j < columnCount; j++) {

if (chocolate[i][j] == chocolate[i + 1][j]) { okRow = false; break; }

}

if (okRow) return true;

}

return false;

}

private boolean BreakColumn(int[][] chocolate, int rowCount, int columnCount) {

for (int i = 0; i < columnCount - 1; i++) {

boolean okColumn = true;

for (int j = 0; j < rowCount; j++) {

if (chocolate[j][i] == chocolate[j][i + 1]) { okColumn = false; break; }

}

if (okColumn) return true;

}

return false;

}

Решение

Для решения данной задачи нужно представить шоколадку как двухмерный массив и проверить, можно ли разломать плитку шоколада ровно, то есть одинаковое ли количество «строк» и «столбцов» шоколада. Если так, то возвращается значение true и false в обратном случае.Для этого были созданы функции BreakRow и BreakColumn с возвращаемым значением типа boolean. Затем стоит проверить возвращаемое значение. Если одна из функций принимает значение true, то выводим положительный ответ. В противном случае ответ отрицательный.

Ссылки

Ссылка на E-olymp
Ссылка на решение

e-olymp112.Торт

27/12/2018 by Илья Черноморец

В честь дня рождения наследника Тутти королевский повар приготовил огромный праздничный торт, который был подан на стол Трем Толстякам. Первый толстяк сам мог бы целиком его съесть за $t_1$ часов, второй — за $t_2$ часов, а третий — за $t_3$ часов.

Сколько времени потребуется толстякам, чтобы съесть весь праздничный торт вместе?

Входные данные

Единственная строка содержит три целых неотрицетельных числа $t_1$, $t_2$ и $t_3$, каждое из которых не превосходит $1000$.

Выходные данные

Вывести время в часах, за которое толстяки вместе могут съесть торт. Результат округлить до двух десятичных знаков.

Тесты

$t_1$	$t_2$	$t_3$	$t$
3	3	3	1.00
4	67	50	3.51
228.22	8	2.28	1.76
1577	157.7	15.77	14.21

С ветвлением

import java.util.*;
import java.lang.*;
import java.io.*;

class Main
{
	public static void main (String[] args) throws java.lang.Exception
	{
		java.util.Scanner i = new java.util.Scanner(System.in);
		double t1 = i.nextDouble();
		double t2 = i.nextDouble();
		double t3 = i.nextDouble();
		double t;
		t = (t1*t2*t3) / (t1*t2 + t1*t3 + t2*t3);
		if(t1*t2*t3 == 0) System.out.println(t);
		else System.out.printf("%.2f",t);
	}
}

import java.util.*;

import java.lang.*;

import java.io.*;

class Main

{

public static void main (String[] args) throws java.lang.Exception

{

java.util.Scanner i = new java.util.Scanner(System.in);

double t1 = i.nextDouble();

double t2 = i.nextDouble();

double t3 = i.nextDouble();

double t;

t = (t1*t2*t3) / (t1*t2 + t1*t3 + t2*t3);

if(t1*t2*t3 == 0) System.out.println(t);

else System.out.printf("%.2f",t);

}

Без ветвления

import java.util.*;
import java.lang.*;
import java.io.*;

/* Name of the class has to be "Main" only if the class is public. */
class Main
{
	public static void main (String[] args) throws java.lang.Exception
	{
		java.util.Scanner i = new java.util.Scanner(System.in);
		double t1 = i.nextDouble();
		double t2 = i.nextDouble();
		double t3 = i.nextDouble();
		double t = 1 / (1 / t1 + 1 / t2 + 1 / t3) ;
		System.out.printf("%.2f",t);
	}
}

import java.util.*;

import java.lang.*;

import java.io.*;

/* Name of the class has to be "Main" only if the class is public. */

class Main

{

public static void main (String[] args) throws java.lang.Exception

{

java.util.Scanner i = new java.util.Scanner(System.in);

double t1 = i.nextDouble();

double t2 = i.nextDouble();

double t3 = i.nextDouble();

double t = 1 / (1 / t1 + 1 / t2 + 1 / t3) ;

System.out.printf("%.2f",t);

}

Решение с ветвлением

Первый толстяк ест со скоростью один торт за $t_1$ часов. Аналогично и с остальными толстяками. Тогда из торта следует вычесть те части, которые съест каждый, чтобы торта не осталось. Получается уравнение
$1-\frac{t}{t_1}-\frac{t}{t_2}-\frac{t}{t_3}=0;$
$\frac{t}{t_1}+\frac{t}{t_2}+\frac{t}{t_3}=1;$
$\frac{tt_2t_3+tt_1t_3+tt_1t_2}{t_1t_2t_3}=1;$
$t\left(t_1t_2+t_2t_3+t_1t_3\right)=t_1t_2t_3;$
$t = \frac{t_1t_2t_3}{t_1t_2+t_2t_3+t_1t_3};$
Рассматриваем случай, при котором одна из переменных равна нулю, тогда выводим ноль. В противном случае выводим значение $t$ с округлением до сотых.

Решение без ветвления

Так как по условию задачи первый толстяк съедает весь торт за $t_1$ часа, второй — за $t_2$ часа и третий — за $t_3$ часа, то их скорость поедания торта составит $\frac{1}{t_1}$, $\frac{1}{t_2}$ и $\frac{1}{t_3}$ торта в час соответсвенно. Если толстяки будут есть торт одновременно, то в час они будут съедать $\left(\frac{1}{t_1}+\frac{1}{t_2}+\frac{1}{t_3}\right)$ часть торта. Тогда весь торт будет съеден за $\frac{1}{\frac{1}{t_1}+\frac{1}{t_2}+\frac{1}{t_3}}$ часов.
Затем нужно вывести результат, округлённый до двух десятичных знаков.

Ссылки

Ссылка на E-olymp
Ссылка на решение

e-olymp 924. Кольцо

25/12/2018 by Илья Черноморец

Заданы площадь кольца и радиус внешней окружности. Определить радиус внутренней окружности.

Входные данные

В одной строке заданы два вещественных числа: площадь кольца и радиус внешней окружности, величина которой не превышает $100$.

Выходные данные

Вывести радиус внутренней окружности с 2 десятичными знаками.

Тесты

S	$R$	$r$
50.2655	5	3.00
45	8	7.05
73.07	7.7	6.00
83.5	34	33.61

import java.util.*;
import java.lang.*;
import java.io.*;
class Main
{
	public static void main (String[] args) throws java.lang.Exception
	{
		double SR, Sr, r;
    	        double Pi = Math.PI;
    	        java.util.Scanner i = new java.util.Scanner(System.in);
		double S = i.nextDouble();
		double R = i.nextDouble();
		SR = Pi * R * R;
    	        Sr= SR - S;
    	        r=Math.sqrt(Sr/Pi);
    	        System.out.printf("%.2f",r);   	
	}
}

import java.util.*;

import java.lang.*;

import java.io.*;

class Main

{

public static void main (String[] args) throws java.lang.Exception

{

double SR, Sr, r;

double Pi = Math.PI;

java.util.Scanner i = new java.util.Scanner(System.in);

double S = i.nextDouble();

double R = i.nextDouble();

SR = Pi * R * R;

Sr= SR - S;

r=Math.sqrt(Sr/Pi);

System.out.printf("%.2f",r);

}

Решение

Для начала стоит напомнить, что площадь круга вычисляется по формуле $S=\pi R^2$.
С клавиатуры вводится площадь кольца $S$ и радиус большей окружности $R$
Зная значение радиуса большей окружности, можно найти площадь большего круга $S_R = \pi R^2$
Зная, что площадь малого круга и площадь кольца образуют площадь большого круга, найдём площадь малого круга $S_r = S_R — S$
Далее находим радиус малой окружности $r$ по формуле $r=\sqrt\frac{S_r}{\pi}$

Ссылки

Ссылка на E-olymp
Ссылка на решение