Мне предоставили реализовать класс, который наследует SegmentedArray и характеризуется следующим:
- принимает большой массив
- частые запросы get(), min();
Поскольку команда set задает значение на интервале, я решил сделать «дерево отрезков». Которое устроено как бинарное дерево относительно индекса (в задании большое количество запросов get(), следовательно будет быстрее искать элемент по индексу), имея в себе левый и правые концы интервала, а также значение на этом интервале.
Основная операция в данной структуре — set(). И она самая сложная по своей схеме. Когда приходить запрос на установление значения на интервале, надо проверить, возможно узел пуст, следовательно такого интервала еще не задавали, и тогда можно его создать. Если же узел не пуст, то надо проверить, в данном узле ли задается наш интервал, или же надо перейти к другому. Если же в данном узле надо задать интервал, то у нас вырисовывается три ситуации: когда задаваемый интервал не превосходит интервала узла, когда заданный интервал превосходить интервал узла и когда одна точка заданного интервала лежит внутри интервала узла, а другая, вне его. В первом случаем, просто разбиваем внутренний интервал на три подинтервала: левая часть внутреннего интервала, заданный интервал и правая часть внутреннего интервала. Во-втором, необходимо увеличить границы внутреннего интервала до задаваемого, и удалить все интервалы(в левом и правом узлах), которые данный новый интервал перекрыл. В третьем необходимо разбить интервал узла на подинтервал до внутренней точки задаваемого интервала, и на то, что осталось. Потом удалить все интервала, которые мы перекрыли.
Метод поиска значение по индексу осуществляется как и в бинарном дереве, пока не попадем на нужный нам интервал, или значение данного индекса еще не было установлено.
Метод нахождения минимума на подинтервала спускается по дереву, пока не попадет на нужный интервал, и потом проверяет значения на каждом из интервалов и выбирает минимальный.
Поскольку у нас дерево отсортировано по индексу, то искать индекс элемента по значению сложнее, необходимо пройти все интервалы от индекса, который нам дали в начале, пока не встретим искомое значение, или же выведем, что его нет.
Теоретическая оценка сложности методов:
- get(i): O(log(count(set)));
- set(x, y, val): O(log(count(set)));
- indexof(val, index): O(count(set() — interval(index)));
- min(x, y) : O(count(set()))
|
1 2 3 4 5 6 |
Первый Set в BigSegmentedArray отрабатывает за 436345 нс. Get в BigSegmentedArray отрабатывает за 7700 нс. 14 Второй Set в BigSegmentedArray отрабатывает за 4991 нс. Min в BigSegmentedArray отрабатывает за 17883 нс. 1 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 |
/** * Created by green on 28.11.15. */ import jdk.internal.org.objectweb.asm.tree.analysis.Value; import java.security.Key; /** * Created by green on 26.11.15. */ interface SegmentedArray<T> { /** * <p>Get value by element index</p> * @param index index of element. * @return Value of element with specified index. */ T get(int index); /** * <p>Set the same value for all elements in the specified index range</p> * @param start the beginning index, inclusive. * @param end the ending index, exclusive. * @param value value for. */ void set(int start, int end, T value); /** * <p>Returns the index within this array of the first occurrence of the specified value, * starting at the specified index. If no such value of k exists, then -1 is returned.</p> * @param value the T-based value for which to search. * @param fromIndex the index from which to start the search. * @return the index within this array of the first occurrence of the element with specified value, * starting at the specified index. */ int indexOf(T value, int fromIndex); /** * <p>Find minimum value in the specified indexes range</p> * @param start the beginning index, inclusive. * @param end the ending index, exclusive. * @return Minimum value. */ T minValue(int start, int end); } class CT <Value extends Comparable<Value>> implements SegmentedArray<Value>{ private class Node { Value value; int l, r; Node left, right, father; public Node (Value value, Node father, int l, int r) { this.value = value; this.left = this.right = null; this.father = father; this.l = l; this.r = r; } } private Node root; private Node add (Node node,Value value, Node father, int l, int r){ if (node == null){ Node newnode = new Node(value,father, l , r); return newnode; } //int compareResultl = l.compareTo(node.l); //int compareResultr = r.compareTo(node.r); if(l > node.r){ node.right = add(node.right, value, node, l, r); }else if(r < node.l){ node.left = add(node.left, value, node, l, r); }else if(l >= node.l && r <= node.r){ if(l == node.l && r == node.r){ node.value = value; return node; }else if(l == node.l){ node.right = add(node.right, node.value, node, r+1, node.r); node.value = value; node.r = r; }else if(r == node.r){ node.left = add(node.left, node.value, node, node.l, l-1); node.value = value; node.l = l; }else{ Node newnode = new Node(value,father, l , r); newnode.left = node.left; newnode.right = node.right; newnode.left = add(newnode.left, node.value, newnode, node.l, l-1); newnode.right = add(newnode.right, node.value, newnode, r+1, node.r); node = newnode; } }else if(l < node.l && r > node.r){ node.value = value; node.l = l; node.r = r; node.left = delete(node.left, l, false); node.right = delete(node.right, r, true); }else if(l < node.l){ if(r == node.r){ node.value = value; node.l = l; node.left = delete(node.left, l, false); }else{ node = add(node, node.value, father, r+1, node.r); node = add(node, value, father, l, r); } }else if (r > node.r) { if (l == node.l) { node.value = value; node.r = r; node.right = delete(node.right, r, true); } else { node = add(node, node.value, father, node.l, l - 1); node = add(node, value, father, l, r); } } return node; } public void set(int l, int r, Value value) { root = add(root, value, null, l, r); } private Node delete(Node node, int d, Boolean side){ if(node == null) return null; if(d < node.r && d > node.l){ node = add(node, node.value, node.father, node.l, d - 1); node = delete(node, d, side); }else if(d < node.l){ if(side) node.left = delete(node.left, d, side); else { node = node.left; node = delete(node, d, side); } }else if(d > node.r){ if(side) { node = node.right; node = delete(node, d, side); }else node.right = delete(node.right, d, side); }else if(d == node.r){ if(side) {node = node.right;} else {node.right = null;node.r = d - 1;} }else if(d == node.l){ if(side) {node.left = null;node.l = d + 1;} else {node = node.left;} } return node; } private Value get(Node node, int index){ if(node == null) return null; if(index > node.r) return get(node.right, index); else if (index < node.l) return get(node.left, index); else return node.value; } public Value get(int index) { return get(root, index); } private Value minimum(Value x, Value y){ if(x == null && y == null) return null; else if(x == null) return y; else if(y == null) return x; else { if (x.compareTo(y) == 1) return y; else return x; } } private Value min(Node node, int start, int end){ if(node == null) return null; if(end < node.l){ return min(node.left, start, end); }else if (start > node.r){ return min(node.right, start, end); }else{ Value v1 = null, v2 = null; if(start < node.l) v1 = min(node.left, start, end); if(end > node.r) v2 = min(node.right, start, end); return minimum(v2, minimum(node.value, v1)); } } public Value minValue(int start, int end){ return min(root, start, end); } private Integer indexOf(Node node, Value value, int index){ if(node == null) return null; if(index <= node.r) { Integer v = null; if(index < node.l){ v = indexOf(node.left, value, index); if (v != null) return v; } if (value == node.value) return Math.max(node.l, index); v = indexOf(node.right, value, index); if (v != null) return v; } return indexOf(node.right, value, index); } public int indexOf(Value value, int index){ return indexOf(root, value, index); } private void print(Node node, int level) { if (node != null) { print(node.right,level+1); for (int i=0;i<level;i++) { System.out.print("\t"); } System.out.println(node.l + "-" + node.r + "->" + node.value); print(node.left,level+1); } } public void print() { print(root,0); } } public class Tree_cut { public static void main(String[] args) { CT<Integer> tree = new CT<>(); long start, end; start = System.nanoTime(); tree.set(50, 4566, 14); //tree.set(130, 740, 29012); //tree.set(1000, 1084, -2); //tree.set(3006, 3070, 51); end = System.nanoTime();//tree.set(50, 4566, 14); System.out.println("Первый Set в BigSegmentedArray отрабатывает за " + (end - start) + " нс."); start = System.nanoTime(); Integer get = tree.get(111); end = System.nanoTime(); System.out.println("Get в BigSegmentedArray отрабатывает за " + (end - start) + " нс."); System.out.println(get); start = System.nanoTime(); tree.set(76, 830, 1); end = System.nanoTime(); System.out.println("Второй Set в BigSegmentedArray отрабатывает за " + (end - start) + " нс."); tree.set(60, 92, 0); start = System.nanoTime(); int minimum = tree.minValue(130, 1400); end = System.nanoTime(); System.out.println("Min в BigSegmentedArray отрабатывает за " + (end - start) + " нс."); System.out.println(minimum); tree.print(); } } |

Замечания:
1) Почему у Вас все индексы класса Integer, а не Int — это ведь замедляет выполнение программы, в чем смысл этого?
2) по оформлению:
а) не хватает тестового вывода,
б) не хватает ссылки на ideone.
3) а вот теперь с содержанием: пояснение гораздо легче бы читалось, если был бы какой-то поясняющий рисунок. Может у Вас получится построить или найти в интернете или применить какой-либо визуализатор структур данных — например визуализатор двоичных деревьев. Вы могли бы показать для примера какое дерево получается.
4) Хотя я и не очень вчитывался, но все же — одна из ключевых Ваших операций — это поиск минимума. Пускай Вы ищете минимум во всем массиве. Это точно займет O(log(count(set()))) операций (я правильно расшифровал это как логарифм от количества операций set)?
По первому пункту вы правы, поменял как надо, что ускорило структуру.
Оформил.
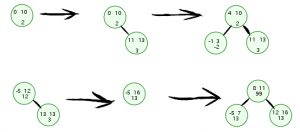
Нарисовал картинку в онлайн фотошопе, в которой изобразил все три ситуации, описанные в данном посте.
Да, вы правильно поняли, зависит от количества функций set и без логарифма,а на данном промежутке, но это мелочь, так то пусть будет просто от количества set. Его можно оптимизировать, добавив балансировку и избавившись еще от пары этапных моментов. Но количество set у нас не большое, так что структура будет работать быстро и экономно.