Задача
Амелия изучает моделирование. Она увлекается моделями с подвижными деталями.
В качестве своего первого задания она сделала прямоугольную коробку размером $2 × n$, которая содержит две параллельные рейки и прямоугольный брусок на каждой из них. Короткий брусок имеет размер $1 × a$, а длинный имеет размер $1 × b$. Длинный брусок имеет стопор на каждом конце, а короткий всегда находится между этими двумя стопорами.
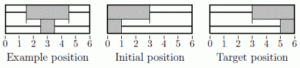
Бруски могут перемещаться вдоль направляющих, по одному стержню за раз, пока короткий брусок находится между стопорами. Таким образом, на каждом движении Амелия выбирает один из брусков и перемещает его, в то время как другой остается на месте.
Первоначально, оба бруска выровнены по одной стороне коробки, и Амелия хочет, чтобы они были выровнены по другой стороне за как можно меньшее количество ходов. Какое минимальное количество ходов она должна сделать, чтобы достичь своей цели?
Входные данные
Три целых числа $a$, $b$ и $n$ $($$1$ $\leqslant$ $a$ $<$ $b$ $\leqslant$ $n$ $\leqslant$ $10$$7$$)$.
Выходные данные
Вывести одно целое число — минимальное количество ходов, которое должна сделать Амелия.
Тесты
№ |
Входные данные |
Выходные данные |
| 1 | 1 3 6 | 5 |
| 2 | 2 4 9 | 7 |
| 3 | 13 45 153 | 9 |
| 4 | 4 16 43 | 7 |
Код программы
|
1 2 3 4 5 6 7 8 9 10 |
class Main { public static void main (String[] args) { java.util.Scanner in = new java.util.Scanner(System.in); int a = in.nextInt(), b = in.nextInt(), n = in.nextInt(), k; k = (int)Math.ceil((double)(n - b) / (b - a)); System.out.println(2 * k + 1); } } |
Решение
Ответом к задаче будет суммарное количество перемещений длинного и короткого брусков. Так как нужно найти минимальное количество ходов, то будем поочередно перемещать бруски на максимальное расстояние.
Длинный брусок, что бы он оказался в конце коробки, суммарно нужно переместить на $n-b$. Каждый раз мы перемещаем его на $b-a$ (необходимое расстояние что бы левые концы брусков совпали и дальше перемещать его было невозможно). Тогда количество перемещений длинного бруска это результат деления всего расстояния $n-b$ на шаг $b-a$. Так как в результате может выйти нецелое число, результат необходимо округлить до большего целого. Обозначим это число как $k =\lceil $$\frac{n-b}{b-a}\rceil$.
Короткий брусок каждый раз будем перемещать до совпадения правых концов брусков. Он будет «догонять» длинный брусок и сделает на один ход больше чем длинный, так как короткий брусок всегда делает первый и последний ход.
Тогда суммарное количество ходов будет $2k+1$.
Ссылки
Условие задачи на e-olymp
Код программы на ideone
