Задача

Лаурел и Харди — два известных киногероя $50$-ых. Они известны своей разницей в весе, как можно увидеть на картинке. Если Вы еще не разобрались, кто из них кто, то я добавлю, что Лаурел легче. В свои юношеские годы Лаурел и Харди любили играть со странными качелями, и когда качели находились в равновесии, то Харди всегда был у земли. Мы рассмотрим двумерную версию качель.
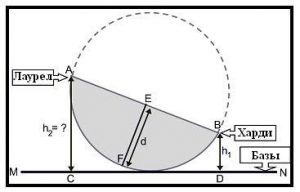
Качели, которыми пользовались Лаурел и Харди, представляют собой часть окружности радиуса $r$, как показано на картинке (они закрашены серым и имеют вид буквы $D$). Харди сел на точку $B$ (самая правая точка качель), а Лаурел сел на точку $A$ (самая левая точка отрезка $AB$). $d = EF$ — расстояние между центром отрезка $AB$ и дуги $AFB$. То есть $E$ — середина отрезка $AB$, а $F$ — середина дуги $AFB$. $MN$ — основа качель, является горизонтальной прямой. $BD = h_1$ — расстояние от Харди до земли. Вам необходимо найти расстояние от Лаурела до земли (обозначаемое $h_2 = AC$).
Входные данные
Первая строка содержит количество тестов $N \space (0 < N ≤ 1000)$. Каждая из следующих $N$ строк представляет собой отдельный тест, который имеет следующий формат:
Каждая строка содержит три целых числа $r \space (10 ≤ r ≤ 100), \space$ $d \space (5 ≤ d ≤ r), \space$ $h_1 \space (5 ≤ h_1 ≤ d)$. Значение этих чисел приведено выше.
Выходные данные
Для каждого теста в отдельной строке вывести его номер и действительной число — значение $h_2$. Это число должно содержать четыре десятичных знака. Формат вывода приведен в примере.
Тесты
| Входные данные | Выходные данные |
|
2 10 10 10 10 7 6 |
Case 1: 10.0000 Case 2: 8.0342 |
|
3 12 7 7 11 11 8 54 12 6 |
Case 1: 7.0000 Case 2: 14.0000 Case 3: 19.7383 |
|
5 94 21 12 23 9 8 5 4 3 2 2 1 43 26 20 |
Case 1: 32.1226 Case 2: 10.0439 Case 3: 5.0440 Case 4: 3.0000 Case 5: 32.4231 |
Код программы
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
import java.io.*; import java.util.*; public class Main { public static void main(String[] args) { Scanner in = new Scanner(System.in); PrintWriter out = new PrintWriter(System.out); short N = in.nextShort(); double r, d, h_1, a, b; for (int i = 1; i <= N; i++){ r = in.nextDouble(); d = in.nextDouble(); h_1 = in.nextDouble(); out.print("Case " + i + ": "); a = Math.asin((r - h_1) / r) - Math.asin((r - d) / r); if (a == 0){ out.format("%.4f%n", h_1); } else{ b = 2 * Math.sqrt(r*r - (r - d) * (r - d)) + h_1 / Math.sin(a); out.format("%.4f%n", b * Math.sin(a)); } } out.flush(); } } |
Решение
Для лучшего понимания решения данной задачи, я построил к ней чертеж, который вы можете видеть сверху. Но прежде чем приступить непосредственно к объяснению решения, я хотел бы обратить внимание на то, что мой рисунок (даже без дополнительных построений) немного отличается от данного нам в условии. Эти различия преднамеренны и метод решения справедлив для обоих рисунков.
В $10$ строке введем число $N$ из входного потока, а в $12$ — запустим цикл, который будет работать $N$ раз. Далее за каждый проход цикла будем читать по $3$ следующих числа из входного потока и выводить на экран номер текущего теста. Перед тем, как идти дальше, разберемся в рисунке. Так как по условию отрезок $EF$ делит сегмент $AFB$ пополам, то по свойствам хорд и дуг окружности, он является частью радиуса $r$ нашей окружности с центром в точке $O$ и перпендикулярен хорде $AB$, что и показано на чертеже. Кроме того, я дорисовал радиусы $OA$ и $OB$ окружности к соответствующим точкам и начертил отрезок $BH$, как продолжение $AB$, от точки $B$ до прямой $MN$. Также, я построил прямоугольный треугольник $\triangle OGB$, в котором катет $OG = r-BD$.
Достроив все необходимые отрезки, легко заметить, что мы имеем прямоугольный треугольник $\triangle ACH$ с катетом $AC$, длину которого нам и нужно найти по условию задачи. Предлагаю сделать это, воспользовавшись формулой $AC = AH \cdot \sin(\angle AHC)$. Найдем значения сомножителей.
Из рисунка очевидно, что $\angle AHC = \angle BHD = \angle EBG = \angle OBG-\angle OBE.$
Сначала найдем $\angle OBG$. Для этого рассмотрим треугольник $\triangle OGB$. Длины его гипотенузы и противолежащего к искомому углу катета нам уже известны, так что можем сразу найти $\angle OBG = \arcsin \frac{OG}{OB}$.
Теперь найдем $\angle OBE$. Рассмотрим прямоугольный треугольник $\triangle OEB$. В нем противолежащий искомому углу катет $OE = r-d$, а гипотенуза $OB = r$. Значит, $\angle OBE = \arcsin \frac{OE}{OB}$.
В итоге остаётся только найти разницу этих углов, которая и будет являться величиной искомого $\angle AHC$. В коде же значение этого угла считается в $17$ строке и присваивается переменной
a .
Стоит заметить, что если $\angle OBG-\angle OBE = 0$, то длины отрезков $AC$ и $BD$, очевидно, совпадают. В таком случае можем сразу вывести на экран $h_2 = h_1$, как мы и поступили в $19$ строке, и перейти к нахождению $AC$ уже для следующего тестового случая.
Если же величина $\angle AHC$ отлична от $0$, то нам все еще предстоит посчитать длину гипотенузы $AH$ треугольника $\triangle ACH$. Она состоит из хорды $AB$ и отрезка $BH$.
Сперва найдем длину хорды. Известно, что $OF$ делит ее на $2$ одинаковых по длине отрезка, значит, следует опять рассмотреть треугольник $\triangle OEB$. Длину его гипотенузы и одного из катетов мы уже находили, так что просто применим теорему Пифагора и найдем $EB = \sqrt{OB^2-OE^2}$. Тогда $AB = 2 \cdot EB$.
Для нахождения длины $BH$, рассмотрим треугольник $\triangle BDH$, в котором этот отрезок является гипотенузой. Длину катета $BD$ и величину угла $\angle BHD$ мы уже знаем, значит, можем применить формулу $BH = \frac{BD}{\sin(\angle BHD)}$.
Сложим найденные значения длин хорды $AB$ и отрезка $BH$, чтобы получить $AH$. В коде эта длина находится в $22$ строке и присваивается переменной
b .
Теперь остается только подставить найденные значения в ранее приведенную формулу и получить наконец длину $h_2$, которую выведем на экран в $23$ строке.
Ссылки
Условие задачи на e-olymp
Код решения на Ideone
Решение этой же задачи на C++
